- Sensoren
- Kraftsensoren
- Drehmomentsensoren
- Dehnungsaufnehmer
- Wegsensoren
- Beschleunigungssensoren
- Temperatursensoren
- Sensorzubehör
- K6D-Zubehör
- Klemmkasten
- Sensor-Configuration
- AS28 Zubehör
- K3R-Zubehör
- K3D-Zubehör
- KM38-Zubehör
- Messkoffer
- PCB Zubehör
- KDs Zubehör
- KR Zubehör
- KMz Zubehör
- END-OF-LIFE Sensoren
- Elektronik
- Dehnungsmessstreifen
- Folien-DMS
- Halbleiter-DMS
- DMS-Zubehör
- Widerstände
- Folien und Klebebänder
- Zubehör-Set
- DMS-Klebstoffe
- Oberflächen-Reinigung
- DMS-Abdeckmittel
- DMS-Lötstützpunkte
- Drähte und Litzen
- DMS-Werkzeuge
- Lötzinn und Flussmittel
- END-OF-LIFE DMS
- Grundlagen
- Grundlagen Sensoren
- Grundlagen Messelektronik
- Grundlagen Dehnungsmessstreifen
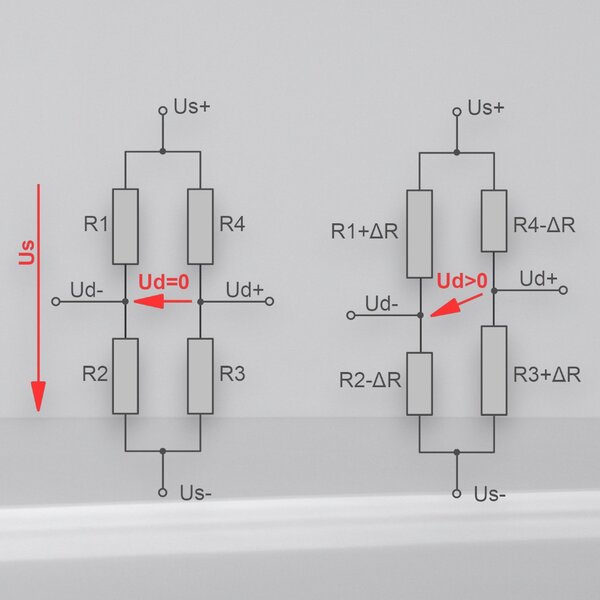
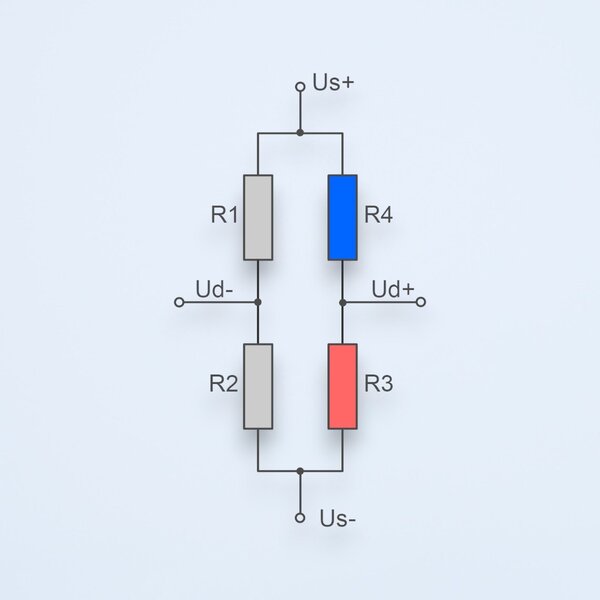
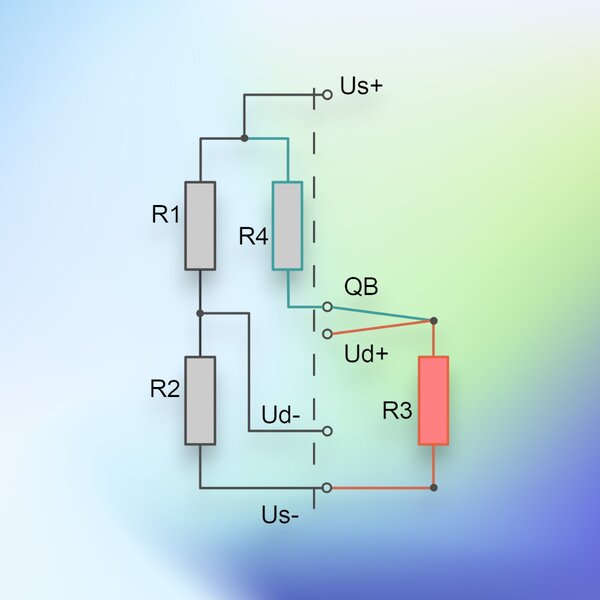
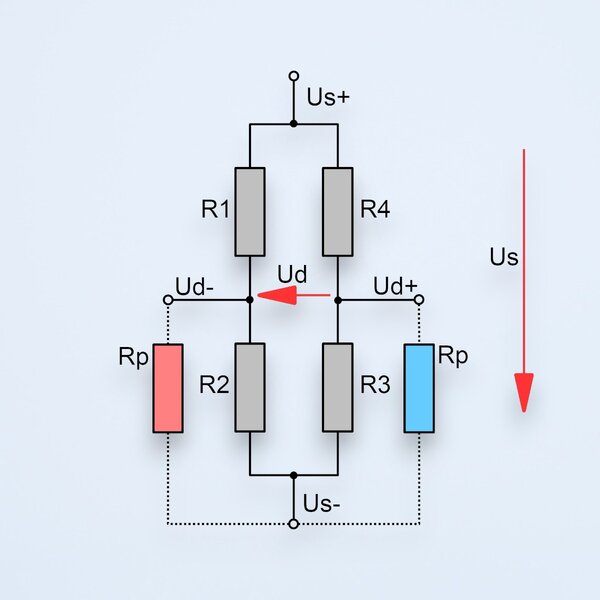
- Wheatstone Brückenschaltung
- Wheatstone Schaltungsvarianten
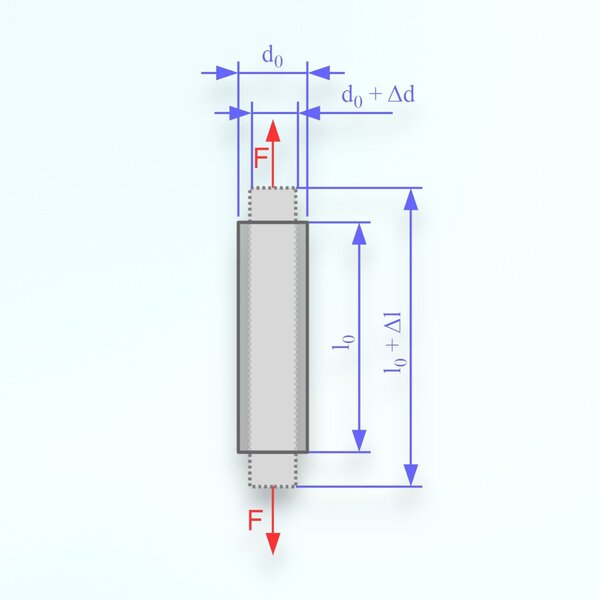
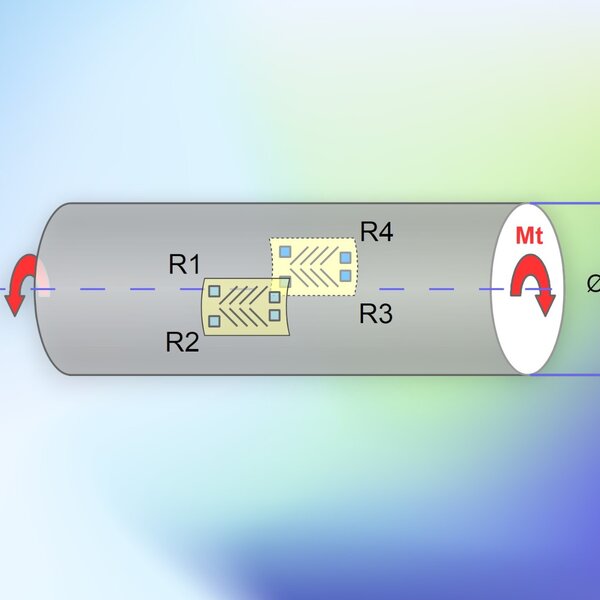
- Spannungsanalyse mit Dehnungsmessstreifen
- Auswahl von Dehnungsmessstreifen
- Grundausstattung DMS Zubehör
- Verdrahtungspläne
- Shuntkalibrierung
- Rissmessstreifen
- Kataloge
- Literatur
- Einheiten Umrechnung
- Kraft
- Masse
- Länge
- Temperatur
- Dehnung
- Drehmoment
- Druck
- Beschleunigung
- Winkelbeschleunigung
- Titer (Textilien)
- Kalibrierung